Contrapunctus XIII from the Art of the Fugue - The Mirror (Inversion) Labyrinth

The Mirror (Inversion) Labyrinth

Bach must work at several levels to be able to create invertible fugues. The first one is the melodic level, a problem he solved when creating the subject.

The subject begins with a D minor arpeggio. The imitation is at the fifth (starts on A, not on D), so the D minor arpeggio transforms into another D minor arpeggio:

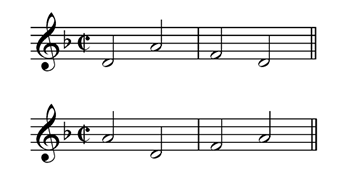
The ascending seconds motive that follows leads - in both versions - from dominant to tonic:

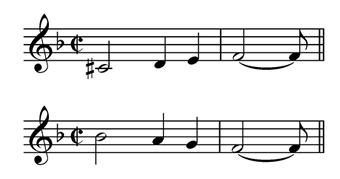
As does the descending seconds that end the subject:

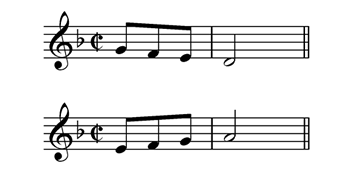
Modulations

Bach must also deal with the harmonic level by inverting the modulations. In the rectus version, the second answer is in the dominant key (A minor). The inversus uses the subdominant key (G minor). In measure 26, the rectus goes to Bb major (submediant) while the inversus goes to F major (mediant):

R e c t u s			Submediant Bb major VI
R e c t u s		Dominant A minor v
	Tonic D minor i
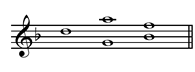I n v e r s u s		Subdominant G minor iv
I n v e r s u s			Mediant F major III

It is very useful to use a guide to show how each note is transformed by the mirror inversion:

The episode that begins in measure 13 starts in the G minor key in the rectus and in A minor in the inversus and both meet at D minor. We will analyze measures 13 to 17 step by step. Make sure that you are able to see the complete image and text, you may need to play with your browser's window and text size. Use the arrow buttons beside the text to move ahead or backwards:

The blue box indicates the rectus version, the red box the inversus. We will focus on two voices: the soprano from the rectus that will be inverted by the bass in the inversus and the bass from the rectus that will be inverted by the alto in the inversus. A simplified version of these voices is shown in the lower staves. By analyzing these voices we will be able to find out how does Bach does his magic...

Rectus		Inversus
Note	Function	Inverts into	Note	Function
E (soprano)	A minor's fifth	<->	G (bass)	G minor's root
A (bass)	A minor's root	<->	D (alto)	G minor's fifth
C (alto)	A minor's third	<->	Bb (soprano)	G minor's third

Rectus		Inversus
Note	Function	Inverts into	Note	Function
C# (soprano)	D minor's leading tone	<->	Bb (bass)	seventh of F major's dominant
G (bass)	seventh of D minor's dominant	<->	E (alto)	F major's leading tone

Rectus		Inversus
Note	Function	Inverts into	Note	Function
C (soprano)	seventh of G minor's dominant	<->	B (bass)	C major's leading tone
F# (bass)	G minor's leading tone	<->	F (alto)	seventh of C major's dominant

Rectus		Inversus
Note	Function	Inverts into	Note	Function
B (soprano)	C major's leading tone	<->	C (bass)	seventh of G minor's dominant
F (bass)	seventh of C major's dominant	<->	F# (alto)	G minor's leading tone

Rectus		Inversus
Note	Function	Inverts into	Note	Function
Bb (soprano)	seventh of C major's dominant	<->	C# (bass)	D minor's leading tone
E (bass)	F major's leading tone	<->	G (alto)	seventh of D minor's dominant

D	E	F	G	A	B	C
G minor's fifth	A minor's fifth	G's leading tone (#)	G minor's root	A minor's root	Seventh of F major dominant chord (b)	D's leading tone (#)
D minor's root	F's leading tone	Seventh of C major dominant chord	Seventh of D minor dominant chord (b)	F major's third	C's leading tone (♮)	Seventh of G minor dominant chord
	C major's third	D minor's third			G minor's third (b)	C major's root
		F major's root

Listen to the rectus:

Listen to the inversus:

In measure 19, following the first episode, the alto in the rectus and the soprano in the inversus present the subject in D minor:

Search • Write to us