Cents, powers and logarithms

Cents are based on the mathematical concept of logarithms. Logarithms were introduced by the Scottish mathematician John Napier (1550/4-1617). The name comes from logos (ratio) and arithmós (number). Logarithms are related to powers.

Two to the third power or \( 2^3 \) equals 1 x 2 x 2 x 2:

\( 2^3 = 1 * 2 * 2 * 2 = 8 \)

Two to the fourth power:

\( 2^4 = 1 * 2 * 2 * 2 * 2 = 16 \)

This is a tricky example that shows why we should start with 1:

\( 2^0 = 1 \) (1 multiplied by no 2)

The following figure illustrates the relationship between powers and logarithms:

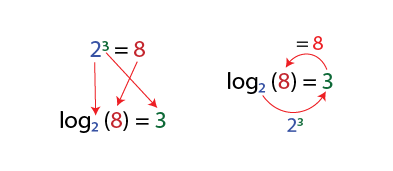
Two, raised to the third power equals 8 ( \( 2 ^ 3 = 8 \) ). The logarithm indicates the power to which we must raise 2 to obtain 8. The second line reads: base 2 logarithm of 8 = 3. In other words, what power do we have to raise 2 (base 2) to get 8? The answer is 3.

In music we use base 2 logarithms because octaves inherently use this base. To find the frequency of a note an octave away, we need to multiply the frequency of the first note by two. Let us take C2 at 60 Hz. This gives us the frequency of C3:

\[ C3 = 60 * 2 = 120 \]

To get to C4, we multiply by 2, twice:

\[ C4 = 60 * 2 * 2 = 240 \]

Or we can use powers:

\[ C4 = 60 * 2^2 = 60 * 4 = 240 \]

The exponent used is related to the number of octaves:

Note	Octaves	Power	Frequency
\[ C2 \]	0	0\[ 2^0 = 1 \]	60 Hz. \[ 60 * 2^0 = 60 * 1 = 60 \]
\[ C3 \]	+1	1\[ 2^1 = 2 \]	120 Hz.\[ C3 = C2 * 2^1 = 60 * 2 = 120 \]
\[ C4 \]	+2	2\[ 2^2 = 4 \]	240 Hz.\[ C4 = C2 * 2^2 = 60 * 4 = 240 \]
\[ C5 \]	+3	3\[ 2^3 = 8 \]	480 Hz.\[ C5 = C2 * 2^3 = 60 * 8 = 480 \]

Let's now use logarithms:

• Let's use the frequencies of C5 (480 Hz.) and C3 (120 Hz.). The notes are at two-octave distance.
• We divide the frequencies and the result is 4:

\( 480 / 120 = 4 \)

• What is the logarithm base 2 of 4, or what power must we raise 2 to get 4? The answer is 2, just as the number of octaves.

\( log_2(4) = 2 \)

• If we multiply C2's frequency \(2^2 \) we get C4's frequency:

\( 120 * 2^2 = 480 \)

We get the same result by subtracting the powers. The power needed to reach C5 from C2 is 3 (see the table above), that of C3 is 1. If we subtract 3 - 1, we get 2, the same result we obtained with \( log_2 (4) = 2 \).

Inadvertently, we are almost at Ellis' formula for the calculation of cents:

We divide the note frequencies and find the base 2 logarithms of the result.

There is just one small detail missing. We will see this in the next section.

It can all be confusing. It is like a labyrinth of mirrors in which it is easy to get lost. You have to go through it many times, with a lot of patience, and little by little you will find your way...

Let's summarize the mathematical concepts learned:

Powers:	\( \color{red}2 \color{blue}^3 \color{black}= 1 * 2 * 2 * 2 = \color{green}8 \)	Multiply 1 by 2 three times
Logarithms:	\( log\color{red}_2 \color{black} ( \color{green}8 \color{black} ) = \color{blue}3 \)	At what power should we raise 2 to get 8?

If you can go from powers to logarithms and vice versa, you can consider the concept understood!

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published by teoria.com.