Temperament Comparison

To compare different tuning systems we will use cents (see What are cents in music?). Each octave can be divided into 1200 cents. In the case of equal temperament, each semitone is 100 cents. In the table below we compare the size of the major third and perfect fifth of the harmonic series with the temperaments discussed:

	Third	Difference	Fifth	Difference
Harmonic series	386		702
Pythagoras	408	+22	702	0
Meantone	386	0	697	-5
Well temperament	390 to 408	+4 to +22	696 or 702	-6 or 0
Equal temperament	400	+14	700	-2

Notes:

• The Pythagorean major third is almost 1/4 semitone larger than the acoustic third.
• The major thirds of the well temperament range from slightly larger (390) than the acoustic third to the size of the Pythagorean major third (408).
• The equal temperament third is larger than the acoustic third, but not as large as the Pythagorean third.
• Equal temperament has smaller fifths than the harmonic series, but they are closer (2 cents) than the meantone (5) or well temperament reduced fifths (6).

The following table compares the tuning systems discussed with equal temperament (horizontal line at 0). The vertical scale is in cents:

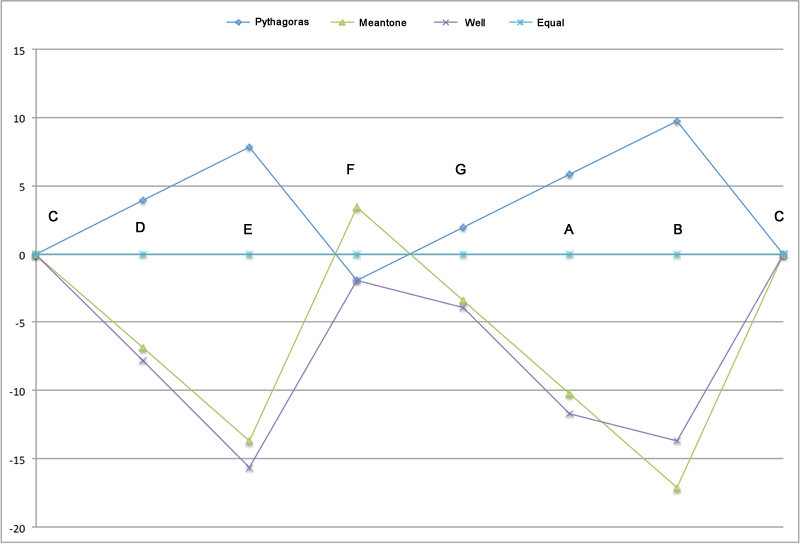
Notes:

• The Meantone tuning (green) is a mirror image of the Pythagorean tuning (blue).
• Equal temperament is a kind of average of the different tuning systems.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published by teoria.com.