2,500 years of musical temperaments
A dialogue between human beings and nature
José Rodríguez Alvira
Pythagorean Tuning
Attributed to Pythagoras (ca. 569 BC - ca. 475 BC), it is the first documented tuning system.
Pythagoras calculated the mathematical ratios of intervals using an instrument called the monochord. If we divide a string into two equal parts and then compare the sound produced by the half part with the sound produced by the whole string, the result is the interval of an octave:

So the mathematical ratio of the octave is 2 to 1.
By dividing the string into 3 equal parts and vibrating 2 of these parts, we obtain the fifth interval:

So the mathematical ratio of the fifth is 3 to 2.
By dividing the string into 4 equal parts and vibrating 3 of these parts we obtain the fourth interval:

So the mathematical ratio of the fourth is 4 to 3.
Using this method, we obtain the same ratios that we calculated using the harmonic series.
Scale Construction
From C we will build a major scale according to the Pythagorean tuning. First, we calculate the fifth by multiplying the frequency of C by 3/2 (the size of the fifth):

To multiply a number by a fraction, we multiply it by the numerator (the top number) and then divide it by the denominator (the bottom number).
G = 261 x 3 / 2.
From G we calculate D by dividing the frequency of G by 4/3 (fourth size):
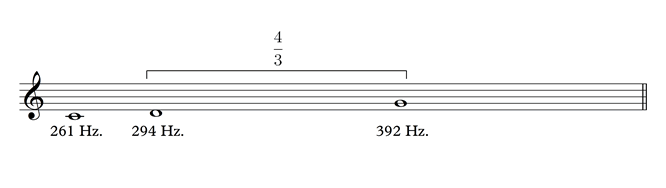
To divide a number by a fraction, we multiply it by the denominator (the lower number) and then divide it by the numerator (the upper number).
Re = 392 x 3 / 4.
Now A (D x 3/2):

Then E (A divided by 4/3):
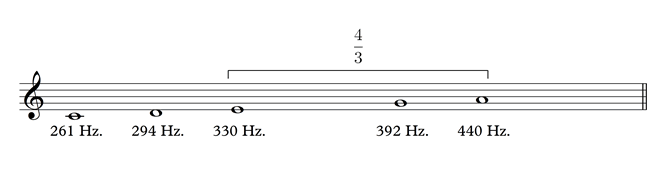
Now B (E x 3/2):
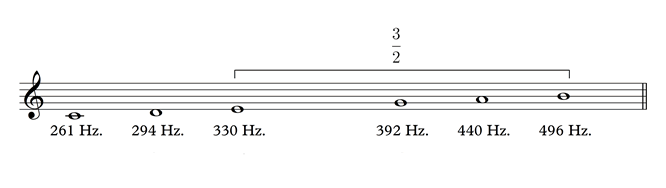
F equals C x 4/3 and C5 is C4 x 2:

Pythagorean tuning remained in use until the Renaissance. What made us look for a new tuning system?
The mathematical ratio of the major third in the harmonic series is 5/4 or 1.25, what is the ratio of the third in the Pythagorean scale? If we divide the frequency of E (330) by C (261), we find that this third is larger than the third in the harmonic series:
330 ÷ 261 = 1.2643678161
Pythagorean tuning was effective when the most commonly used harmonic intervals were the octave, fifth and fourth. With the increasing use of thirds in the Middle Ages and Renaissance, the Pythagorean third was no longer acceptable to many ears. This leads us to look for new tuning systems.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published by teoria.com.